Introduction
The ideal gas law is an equation demonstrating the relationship between temperature, pressure, and volume for gases (see Graph. The Ideal Gas Law). These specific relationships stem from Charles's, Boyle's, and Gay-Lussac's laws. Charles's law identifies the direct proportionality between volume and temperature at constant pressure. Boyle's law identifies the inverse proportionality of pressure and volume at a constant temperature, and Gay-Lussac's law identifies the direct proportionality of pressure and temperature at a constant volume.
Collectively, these laws form the ideal gas law equation: PV=nRT
where P is the pressure, V is the volume, n is the number of moles of gas, R is the universal gas constant, and T is the absolute temperature. The modified version, the Van Der Waals equation, includes a for intermolecular forces and b to represent the volume of 1 mole of molecules. As such, this version better quantifies the behavior of real gases. The universal gas constant R is a number that satisfies the proportionalities of the pressure-volume-temperature relationship. R has different values and units that depend on the pressure, volume, moles, and temperature specifications. Various values are accepted for R through online databases, or dimensional analysis converts the observed units of pressure, volume, moles, and temperature to match a known R-value. As long as the units for pressure, volume, moles, and temperature are consistent, either approach is acceptable. The temperature value in the ideal gas law must be in absolute units, either Rankine (°R) or Kelvin (K), to prevent the right-hand side of the equation from being zero, which violates the pressure-volume-temperature relationship. The conversion from Fahrenheit (F) or Celsius (C) to absolute temperature units is a simple addition of a fixed value to the Fahrenheit (F) or the Celsius (C) temperature—°R=F+459.67 and K=C+273.15.
For a gas to be ideal, 4 governing assumptions must be true:
- The gas particles have negligible volume compared to the total volume of a gas.
- The gas particles are equally sized and do not have intermolecular forces, such as attraction or repulsion, with other gas particles.
- The gas particles move randomly in agreement with Newton's laws of motion that describe kinetic energy.
- The gas particles have perfect elastic collisions with no energy loss or gain.
In reality, ideal gases do not exist. Any gas particle possesses a volume within the system (a minute amount, but present nonetheless), violating the first assumption. In addition, gas particles are of different sizes; for example, hydrogen gas is significantly smaller compared to xenon gas. Gas particles in a system exhibit intermolecular forces with adjacent gas particles, especially at low temperatures when the particles do not move quickly and interact with each other. Although gas particles move randomly, they do not have perfect elastic collisions due to the conservation of energy and momentum within the system.[1][2]
Although ideal gases are theoretical constructs, real gases can behave ideally under certain conditions. Real gases behave ideally when subjected to either very low pressures or high temperatures. The low pressure of a system allows the gas particles to experience less intermolecular forces with other gas particles. Similarly, high-temperature systems allow gas particles to move quickly within the system and exhibit less intermolecular forces. Therefore, real gases can be considered ideal for calculation purposes in either low-pressure or high-temperature systems. Some liquids also exhibit the properties of ideal gases.[3][4]
The ideal gas law also holds for a system containing multiple ideal gases, known as an ideal gas mixture. With multiple ideal gases in a system, these particles are still assumed not to have any intermolecular interactions with one another and to meet all criteria of an ideal gas law independently. An ideal gas mixture partitions the system's total pressure into the partial pressure contributions of each gas particle.
Consequently, the previous ideal gas equation can be rewritten as: PiV=niRT
where Pi is the partial pressure of species i and ni are the moles of species i. Gas mixtures are ideal for easy calculation at low-pressure or high-temperature conditions. When systems are not at low pressures or high temperatures, the gas particles interact, inhibiting the ideal gas law accuracy. However, other models, such as the Van der Waals equation of state, account for the volume of the gas particles and the intermolecular interactions. A recent take on the Boltzmann model proposes separate equations for mass and momentum and for total energy to account for the volume of gas particles. These simulations compare ideal gas mixtures to real gas mixtures. Consequently, electrolyte mixtures have been developed in biotechnology and clinical medicine.[5][6]
Function
Register For Free And Read The Full Article
Search engine and full access to all medical articles
10 free questions in your specialty
Free CME/CE Activities
Free daily question in your email
Save favorite articles to your dashboard
Emails offering discounts
Learn more about a Subscription to StatPearls Point-of-Care
Function
Despite the existence of more rigorous models for gases, the ideal gas law remains versatile in representing other phases and mixtures. Christensen et al performed a study to create calibration mixtures of oxygen, isoflurane, enflurane, and halothane. These gases are commonly used in anesthetics, which require accurate measurements to ensure patient safety. In this study, Christensen et al compared the ideal gas assumption to more rigorous models to identify the partial pressures of each gas. The ideal gas assumptions had a 0.03% error for the calibration experiment. This study concluded that the error from the ideal gas assumption could be used to tune the calibration of the anesthetics, but the deviation was not appreciable to prevent use on patients.[7][8][9]
Furthermore, the ideal gas law can be used to model the behavior of certain plasmas and gaseous mixtures. In a study by Oxtoby et al, they found that ideal gas could model dusty plasma particles. The study suggests that the similarity between dusty plasma and ideal gas behavior is due to the low compression ratios of dusty plasma. Although more complex models are required, the ideal gas law accurately represents the plasma phase models. Ideal gases have also contributed to the study of surface tension in water. Sega et al proved that the ideal gas contribution to surface tension in water was not trivial but rather finite. Sega et al created a new expression that better represented the ideal gas contribution to surface tension. As a result, the relationship of ideal gases to surface tension better represents gas-liquid interfaces. The ideal gas law also applies to obtain dimensional limitations about a thermodynamic system in the gas-to-liquid transition.[10][11]
Issues of Concern
The main concern with the ideal gas law is that no true ideal gases exist; therefore, the application is theoretical. This limitation is demonstrated by the approach of considering the thermodynamics of an empty box. If all the constraints are set to ideal, then the expected behavior of ideal gases is exhibited. When each parameter of a box is changed, the behavior of real gases is studied.[12] The ideal gas law does not account for chemical reactions in the gaseous phase, which could change the system's pressure, volume, or temperature. This omission is a significant concern, particularly because the pressure can rapidly increase in gaseous reactions and quickly become a safety hazard in real systems.
In reality, gases exist in dynamic systems, and some constraints are variable. When considering the circuitry of the cardiovascular system, parallel and perpendicular resistors consisting of capillaries, veins, and arteries complicate the movement of gas and liquid, leading to complex and occasionally sudden changes in pressure or volume. Alternatively, when considering hemodialysis circuitry, the renal system variables must be translated to facilitate continued electrolyte balances within the body. These are 2 areas where pressure, volume, and temperature are extensively compared in real and ideal conditions. Consequently, the Van der Waals equation of state that considers intermolecular forces and volume is more accurate when modeling real gas systems.
The impact of the size of the system is also under debate, with smaller systems exhibiting more excellent ideal gas behavior due to a finite degree of freedom compared to large systems.[13] To test the size constraint, 2 small systems were studied separately and in proximity to assess deviations from ideal gas assumptions with inconclusive results.[14] Simulations incorporating size show deviations from classical thermodynamics, as demonstrated by the variables of the ideal gas law.[15]
Clinical Significance
Respiratory Physiology
As studied by Christensen et al, the ideal gas law can be used to calibrate anesthetic mixtures with a nominal error. In high-altitude environments, the ideal gas law may be more accurate for monitoring gas flow pressure into patients compared to sea-level conditions. If significant temperature fluctuations occur, the pressure required to deliver oxygen to a patient could be adjusted. These considerations address the inconsistencies between ideal gas behavior and application to a real system. The variables of the ideal gas law make assumptions concerning the exchange of oxygen and carbon dioxide at the alveolar membrane, especially given the proportion of ventilation (V) to perfusion (Q) at different parts of the lungs, from apices to bases. As such, applying classic thermodynamics requires adjustments, accounting for factors such as alveolar dead space, pathological barriers to ideal gas behavior, and the unpredictability of carbon dioxide and oxygen, given fluctuations in volume or temperature. Assuming maximum exchange is possible at all parts of the lungs could limit the ability to oxygenate a patient. A recent study described this variability as V/Q scatter; the impact of V/Q scatter is observed when considering the solubility of anesthetic agents in blood and the distribution difference in different parts of the lungs. In this context, ideal gas behavior is the ideal V/Q ratio based on fixed blood solubility.[16][17]
Applications in Clinical Practice
Many anesthesiology, emergency medicine, critical care, and primary care clinicians utilize gas mixtures for analgesia and sedation. Opioids are a source of substance abuse, and alternatives are being explored. In particular, a fixed nitrous oxide/oxygen mixture has been studied in self-administered delivery, although not yet applicable worldwide.[7] Mixtures of several anesthetics are utilized pre- and postoperatively.[11] The context of gas exchange is also pertinent when considering types of postoperative care in managing and returning patients to baseline levels of function. Relating gas behavior to weight and clinical context is important in mechanical ventilation.[8] In terms of ideal gas behavior, the gas particles interact with real systems, which are dynamic due to the changing parameters of the human body.[9] This dynamic interaction explains why treating clinicians must consider factors such as tidal volume, respiratory rate, and fraction of oxygen to determine how much gas exchange should occur concerning a patient's clinical status.[10][18] Alveolar-arterial oxygen difference is typically calculated using an ideal oxygen partial pressure. However, newer methods consider the alveolar steady state or the end-tidal partial pressure, bridging ideal gas behavior to application.[19]
Enhancing Healthcare Team Outcomes
Understanding ideal gas behavior is crucial for healthcare professionals in various contexts. A thorough understanding of ideal gas behavior empowers healthcare providers to navigate intricate scenarios and make informed decisions regarding patient care. Healthcare professionals with a nuanced understanding of ideal gas behavior can effectively evaluate realistic representations and discern which variables are fixed and which can be manipulated for experimentation.
Although current research is grounded in theories dating back hundreds of years, clinicians should remain familiar with the thermodynamic understanding of pressure, volume, and temperature, especially when delivering medical care in areas such as ventilation, acid-base status, pain management, or sedation. Familiarity with the ideal gas formula can prevent medical errors and optimize patient care.
Furthermore, several opportunities exist to explore the precise delivery of oxygen and carbon dioxide under changing environmental conditions. These areas are most pertinent to clinicians in anesthesiology and critical care, where meticulous attention to gas dynamics can significantly impact patient outcomes and overall quality of care.
Media
(Click Image to Enlarge)
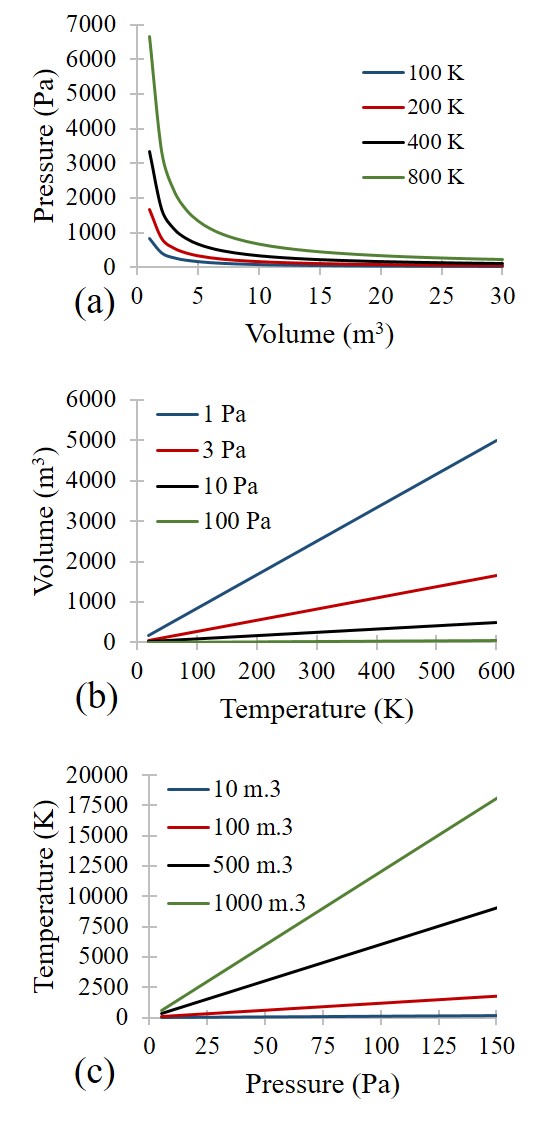
The Ideal Gas Law. These graphs demonstrate the Ideal Gas Law with 1 molecule of gas to show: (a) the change in pressure and volume at constant temperature, (b) the change in temperature and volume at constant pressure, and (c) the change in pressure and temperature at constant volume.
Contributed by KM Tenny
References
Naeiji P, Woo TK, Alavi S, Varaminian F, Ohmura R. Interfacial properties of hydrocarbon/water systems predicted by molecular dynamic simulations. The Journal of chemical physics. 2019 Mar 21:150(11):114703. doi: 10.1063/1.5078739. Epub [PubMed PMID: 30901995]
Rodenburg J, Paliwal S, de Jager M, Bolhuis PG, Dijkstra M, van Roij R. Ratchet-induced variations in bulk states of an active ideal gas. The Journal of chemical physics. 2018 Nov 7:149(17):174910. doi: 10.1063/1.5048698. Epub [PubMed PMID: 30408988]
Huang Y, Widom M. Entropy approximations for simple fluids. Physical review. E. 2024 Mar:109(3-1):034130. doi: 10.1103/PhysRevE.109.034130. Epub [PubMed PMID: 38632758]
Vacula J, Novotný P. Critical pressure in liquids due to dynamic choking. Physical review. E. 2022 Apr:105(4-2):045107. doi: 10.1103/PhysRevE.105.045107. Epub [PubMed PMID: 35590676]
Sawant N, Dorschner B, Karlin IV. A lattice Boltzmann model for reactive mixtures. Philosophical transactions. Series A, Mathematical, physical, and engineering sciences. 2021 Oct 18:379(2208):20200402. doi: 10.1098/rsta.2020.0402. Epub 2021 Aug 30 [PubMed PMID: 34455843]
Mullen JW, Li H, Atkin R, Silvester DS. Mixing Ionic Liquids Affects the Kinetics and Thermodynamics of the Oxygen/Superoxide Redox Couple in the Context of Oxygen Sensing. ACS physical chemistry Au. 2022 Nov 23:2(6):515-526. doi: 10.1021/acsphyschemau.2c00035. Epub 2022 Sep 26 [PubMed PMID: 36855608]
Gao LL, Yang LS, Zhang JJ, Wang YL, Feng K, Ma L, Yu YY, Li Q, Wang QH, Bao JT, Dai YL, Liu Q, Li YX, Yu QJ. A fixed nitrous oxide/oxygen mixture as an analgesic for trauma patients in emergency department: study protocol for a randomized, controlled trial. Trials. 2018 Sep 29:19(1):527. doi: 10.1186/s13063-018-2899-6. Epub 2018 Sep 29 [PubMed PMID: 30268163]
Level 1 (high-level) evidenceDongelmans DA, Veelo DP, Bindels A, Binnekade JM, Koppenol K, Koopmans M, Korevaar JC, Kuiper MA, Schultz MJ. Determinants of tidal volumes with adaptive support ventilation: a multicenter observational study. Anesthesia and analgesia. 2008 Sep:107(3):932-7. doi: 10.1213/ane.0b013e31817f1dcf. Epub [PubMed PMID: 18713908]
Level 2 (mid-level) evidenceWrigge H, Uhlig U, Baumgarten G, Menzenbach J, Zinserling J, Ernst M, Drömann D, Welz A, Uhlig S, Putensen C. Mechanical ventilation strategies and inflammatory responses to cardiac surgery: a prospective randomized clinical trial. Intensive care medicine. 2005 Oct:31(10):1379-87 [PubMed PMID: 16132888]
Level 1 (high-level) evidenceSloan MH, Conard PF, Karsunky PK, Gross JB. Sevoflurane versus isoflurane: induction and recovery characteristics with single-breath inhaled inductions of anesthesia. Anesthesia and analgesia. 1996 Mar:82(3):528-32 [PubMed PMID: 8623956]
Level 1 (high-level) evidenceChristensen PL, Nielsen J, Kann T. Methods to produce calibration mixtures for anesthetic gas monitors and how to perform volumetric calculations on anesthetic gases. Journal of clinical monitoring. 1992 Oct:8(4):279-84 [PubMed PMID: 1453187]
Schmitz GJ, Te Vrugt M, Haug-Warberg T, Ellingsen L, Needham P, Wittkowski R. Thermodynamics of an Empty Box. Entropy (Basel, Switzerland). 2023 Feb 8:25(2):. doi: 10.3390/e25020315. Epub 2023 Feb 8 [PubMed PMID: 36832681]
Naplekov DM, Yanovsky VV. Distribution of energy in the ideal gas that lacks equipartition. Scientific reports. 2023 Feb 28:13(1):3427. doi: 10.1038/s41598-023-30636-6. Epub 2023 Feb 28 [PubMed PMID: 36854979]
Corti DS, Ohadi D, Fariello R, Uline MJ. Microcanonical Thermodynamics of Small Ideal Gas Systems. The journal of physical chemistry. B. 2023 Apr 20:127(15):3431-3442. doi: 10.1021/acs.jpcb.3c00455. Epub 2023 Apr 6 [PubMed PMID: 37022190]
Strøm BA, Bedeaux D, Schnell SK. Adsorption of an Ideal Gas on a Small Spherical Adsorbent. Nanomaterials (Basel, Switzerland). 2021 Feb 9:11(2):. doi: 10.3390/nano11020431. Epub 2021 Feb 9 [PubMed PMID: 33572075]
Peyton PJ. Ideal alveolar gas defined by modal gas exchange in ventilation-perfusion distributions. Journal of applied physiology (Bethesda, Md. : 1985). 2021 Dec 1:131(6):1831-1838. doi: 10.1152/japplphysiol.00597.2021. Epub 2021 Oct 21 [PubMed PMID: 34672764]
Peyton PJ, Hendrickx J, Grouls RJE, Van Zundert A, De Wolf A. End-tidal to Arterial Gradients and Alveolar Deadspace for Anesthetic Agents. Anesthesiology. 2020 Sep:133(3):534-547. doi: 10.1097/ALN.0000000000003445. Epub [PubMed PMID: 32784343]
Karalapillai D, Weinberg L, Peyton P, Ellard L, Hu R, Pearce B, Tan CO, Story D, O'Donnell M, Hamilton P, Oughton C, Galtieri J, Wilson A, Serpa Neto A, Eastwood G, Bellomo R, Jones DA. Effect of Intraoperative Low Tidal Volume vs Conventional Tidal Volume on Postoperative Pulmonary Complications in Patients Undergoing Major Surgery: A Randomized Clinical Trial. JAMA. 2020 Sep 1:324(9):848-858. doi: 10.1001/jama.2020.12866. Epub [PubMed PMID: 32870298]
Level 1 (high-level) evidenceWest JB, Liu MA, Stark PC, Prisk GK. Measuring the efficiency of pulmonary gas exchange using expired gas instead of arterial blood: comparing the "ideal" Po(2) of Riley with end-tidal Po(2). American journal of physiology. Lung cellular and molecular physiology. 2020 Aug 1:319(2):L289-L293. doi: 10.1152/ajplung.00150.2020. Epub 2020 Jun 3 [PubMed PMID: 32491950]