Definition/Introduction
The refraction of light is the bending of light rays as they pass from one medium to another, thereby changing the path of the rays. Refraction occurs due to a change in the speed of the light ray or wave. [1] The speed of light is greatest in a vacuum. When the light rays travel from a rarer to a denser medium, they bend towards the normal. If the light rays travel from a denser to a rarer medium, they bend away from the normal.[2] The greater the density of the media, the higher the refractive index. Snell’s law, or the law of refraction, quantitatively defines the amount of bending of waves dependent on the refractive index of the two media.
The refraction of light has applications in ophthalmic physics. Light refraction in nature is what creates rainbows, optical illusions, the formation of mirages, and the twinkling of stars.[2] The refraction phenomenon also occurs with sound, water, and other waves. Light rays can be bent by spectacle lenses, magnifying glasses, prisms, and water droplets. Without the refraction of light, our eyes may not be able to focus clearly.[3]
Issues of Concern
Register For Free And Read The Full Article
Search engine and full access to all medical articles
10 free questions in your specialty
Free CME/CE Activities
Free daily question in your email
Save favorite articles to your dashboard
Emails offering discounts
Learn more about a Subscription to StatPearls Point-of-Care
Issues of Concern
Refraction Terminology
The normal line, or normal (N), is a line drawn perpendicular to the boundary at the point of incidence. A dotted line usually indicates the normal in a ray diagram. The point of incidence is where the incident ray strikes the boundary between the two media.[4]
The incident ray is the light ray approaching and striking the refracting surface, which occurs at the boundary of two media. After the incident ray strikes the refracting surface, it bends and is now a refracted ray. The angle of incidence (Θi) is defined as the angle between the incident ray and the normal. The angle of refraction (Θr) is the angle between the normal and the refracted ray.[5] The incident and refracted rays are on the opposite sides of normal, and all three vectors align in one plane.
Law of Refraction
The relationship between the angles of incidence and refraction and the indices of refraction of the two media is known as the Law of Refraction or Snell's law.[6] This law applies to the refraction of light in any situation, regardless of what the two media are. The index of refraction of each media (n) is a constant. The index of refraction for a vacuum is 1. The index of refraction for air is so close to 1 that the difference is immeasurable to us.
The incident ray traveling through the incident medium, with a refractive index of ni, strikes the refractive surface of the second medium, with a refractive index of nr, and becomes the refracted ray. Mathematically, this is:
- ni ⋅ sin(Θi) = nr ⋅ sin(Θr)
The critical angle is defined as the angle of incidence that creates an angle of refraction of 90 degrees. It is the largest angle of incidence for which refraction can still occur. Light will undergo total internal reflection for any angle of incidence greater than the critical angle. Total internal reflection will only occur if the incident light ray is in an optically denser medium and approaching an optically rarer medium, and the angle of incidence for the light ray is greater than the critical angle. Optical density is a measure of the tendency of a material to slow down any light traveling through it.[7][8]
Types of Refraction
Refraction Through a Plane Media
When refraction occurs through a plane media, as when light travels through the air across an incident surface like a glass plate, some of the light is reflected off from the surface, and some is transmitted through the surface. The reflected, or emergent, rays (E) are deflected away from the normal line of the incident surface. The incident rays (I) will deflect toward the normal line of the incident surface. This deflection of incident light rays toward the normal in the denser medium (the glass) is responsible for objects appearing nearer than they actually are. Alternatively, when incident rays travel from an optically denser medium to an optically rarer medium, objects will appear further away than they actually are.[9]
When light rays travel from optically rarer to optically denser media, the incident light rays (I) bend towards the normal, and the angle of refraction (Θr) is less than that of the angle of incidence (Θi).[10] When the incident light rays (I) travel from an optically denser to an optically rarer medium, the light rays bend away from the normal, and the angle of refraction (Θr) is greater than the angle of incidence (Θi).[11]
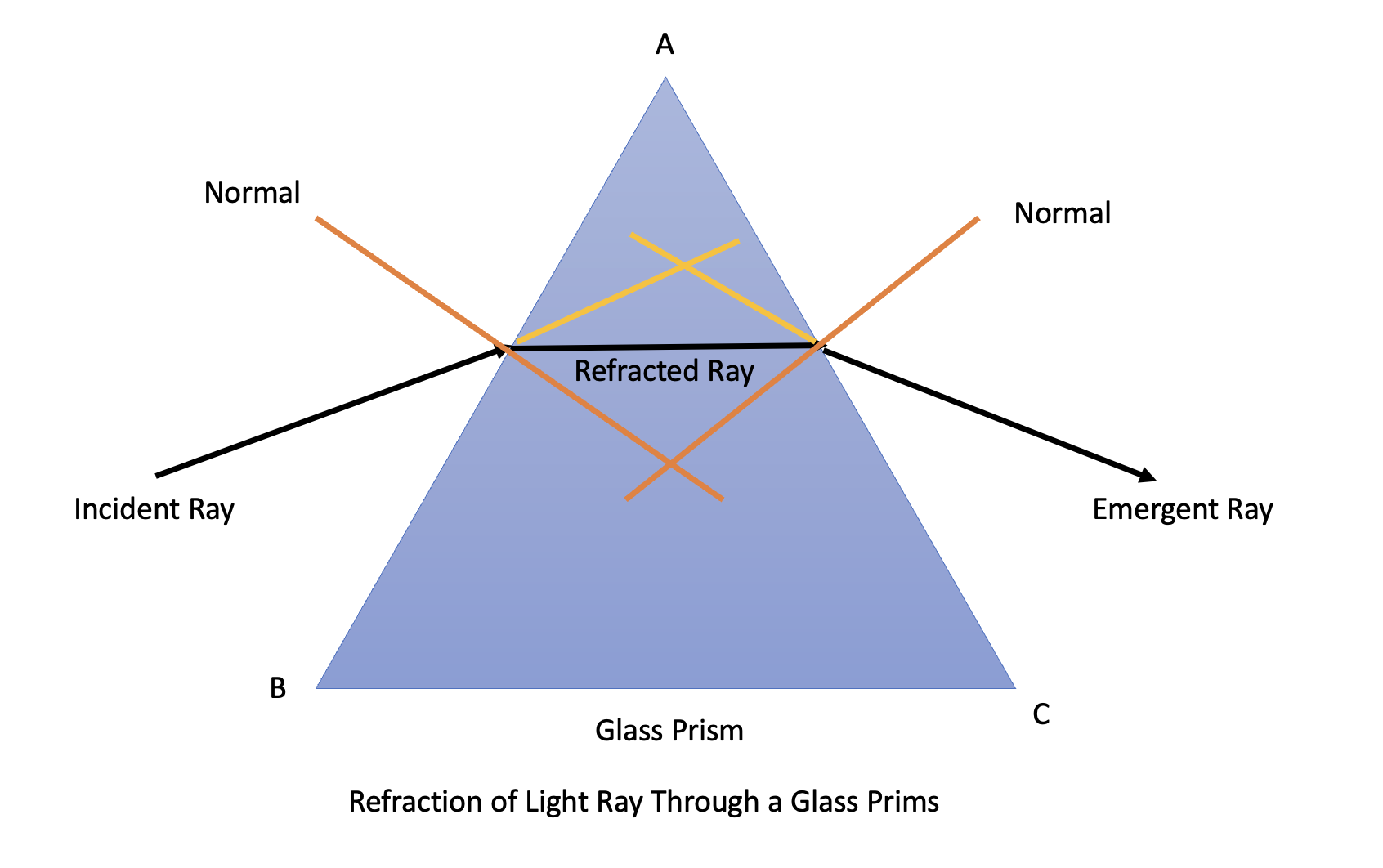
Refraction Through a Prism
A triangular prism is a transparent refracting medium bound by five planar surfaces, each inclined at an angle. The refracting or apical angle is the angle of a prism formed by two adjacent surfaces. The greater the angle between the two surfaces, the more the prismatic effect.
The axis of the prism is a line bisecting the apical angle, and the base of the prism is the surface opposite the apical angle. The orientation of a prism is indicated by the position of the base, whether base-in, base-out, base-up, or base-down.[12]
Light rays passing through a prism follow the fundamental law of refraction at each incident surface, and the incident ray will deviate toward the base of the prism.
The refractive index of a glass prism is defined as:
- η = {Sin[(A + δ)/2]} ÷ sin(A/2), where
- η = refractive index of a glass prism
- A = angle of the prism (angle between the two sides of the reflecting faces of the prism)
- δ = angle of deviation [13]
The angle of deviation is the change in the direction of the incident light ray as it passes through the prism. Mathematically, the angle of deviation is the angle between the incident ray as it passes through the first face of the prism and the refracted emergent ray that emerges from the second face of the prism (Image. Refraction of Light Through a Glass Prism). The angle of deviation is governed by the following:
- μ = material of the prism
- A = angle of the prism
- Θi =angle of incidence of the incident ray
- λ = wavelength of light of the incident ray
The angle of minimum deviation occurs when refraction is symmetrical — when the angle of incidence equals the angle of emergence. The image formed by a prism is upright, virtual, and displaced toward the apex. The power of the prism is denoted in prism diopters and is dictated by the apical prism angle. A 1-diopter prism will displace an object 1 cm at a distance of 1 m. One prism diopter of displacement is central or 0.57 degrees of an arc. When incorporating prism optics into an ophthalmic lens, the following rules apply:
- The amount of correction should be split between both eyes
- Base-out prisms should be prescribed in esodeviations
- Base-in prisms should be prescribed in exodeviations
ATD (apex towards the deviation) is an acronym to remember to prescribe prisms for correcting esodeviations.[14]
Refraction at a Curved Surface
Refraction at a curved surface is essential for ophthalmology because the cornea is a curved convex surface. When rays of light strike a spherical surface separating two transparent media with different refraction indices, the light rays will be refracted in the same plane per the law of refraction. The amount of refraction will depend on the angle of incidence and dioptric power of the spherical surface.[15]
The power of a spherical refracting surface in diopters is equal to the difference in refractive indices of the two media divided by the radius of the curvature. Mathematically, this is:
- D = (n'-n)/r, where
- D = power in diopters
- r = radius of curvature of the refracting surface
- n'= the refraction index of the right side of the surface, assuming a ray moving from left to right
- n = the refractive index of the surface. The sign convention of r is positive to the right of the surface and negative towards the left of the surface.[16]
During retinoscopy, a patient focusing on a near object instead of a far distance might give a pseudo-myopic reading. Focusing on a near object for a longer period results in an accommodative spasm. Refraction may not yield the correct result in these patients.[17]
Clinical Significance
The principles of total internal reflection and prism refraction are used in many clinical instruments such as applanation tonometers, gonioscopes, keratometers, slit-lamp microscopes, and fiberoptic cables.
Fiber Optical Devices
Optical fibers are thin, flexible glass rods that carry light from one end to the other using total internal reflection. A bundle of optical fibers is called a light pipe. An optical fiber consists of a central core graded smoothly into an outer cladding layer with a lower refraction index. This fiber is usually coated in a protective sheath. Only the internally reflected rays are propagated along the fiber. Such fibers form the basis of endoscopes used extensively in gastroenterology, urology, general surgery, and gynecology.[18]
Prisms
Prisms can be used for diagnostic or therapeutic purposes.
Prisms used for diagnostic purposes include unmounted loose prisms, trial lens-mounted prisms, and vertical or horizontal prism bars. Prisms may be used to predict diplopia in children undergoing surgical strabismus correction or to diagnose malingering. The prism cover test and Krimsky test contribute to the objective measurement of the angle of deviation, which can also be measured subjectively using a Moddox rod. The four-prism diopter test can diagnose microtopia, and prisms may also be used to measure fusional reserve.
Prisms also have therapeutic applications, relieving diplopia in patients with decompensated phorias, low hypermetropia, and paralytic strabismus with diplopia in the primary position. In patients with convergence insufficiency, prisms may be used to build up fusional reserve; it is recommended to utilize a base-out prism only during the exercise period.
Prisms for temporary wear include clip-on spectacle prisms and Fresnel prisms. Fresnel prisms are tiny prisms manufactured from plastic sheets that can be adhered to spectacles. However, prisms for permanent wear are inserted into the spectacles by decentering the prescribed spherical lenses. When a spherical correction is not required, prisms can be mounted on the spectacle frame.
Nursing, Allied Health, and Interprofessional Team Interventions
The optometrist, ophthalmologist, optometry technicians, and clinical support staff work in concert to enhance outcomes for patients with refractive error. Open and effective communication among team members ensures that everyone clearly understands the patient's condition and treatment plan. A holistic approach to patient assessment, considering the physical, emotional, social, and environmental factors that can influence vision, promotes patient adherence to treatment plans.
Media
(Click Image to Enlarge)
References
Sutter E, Foster A, Francis V. Optics & refraction. Community eye health. 2000:13(33):8 [PubMed PMID: 17491945]
Sliney DH. What is light? The visible spectrum and beyond. Eye (London, England). 2016 Feb:30(2):222-9. doi: 10.1038/eye.2015.252. Epub 2016 Jan 15 [PubMed PMID: 26768917]
Schechter RJ. Snell's Law: optimum pathway analysis. Survey of ophthalmology. 1977 May-Jun:21(6):464-6 [PubMed PMID: 898012]
Gallegos J, Stokkermans TJ. Refractive Index. StatPearls. 2023 Jan:(): [PubMed PMID: 37276310]
Kaur K, Gurnani B. Subjective Refraction Techniques. StatPearls. 2023 Jan:(): [PubMed PMID: 35593807]
Gould CM. Law of refraction-change following increase or decrease of body-weight. Transactions of the American Ophthalmological Society. 1897:8():115-8 [PubMed PMID: 25259241]
Kneebone R. Total internal reflection: an essay on paradigms. Medical education. 2002 Jun:36(6):514-8 [PubMed PMID: 12047663]
Ma G, Liang R, Wan Z, Wang S. Critical angle reflection imaging for quantification of molecular interactions on glass surface. Nature communications. 2021 Jun 7:12(1):3365. doi: 10.1038/s41467-021-23730-8. Epub 2021 Jun 7 [PubMed PMID: 34099717]
Cheng Q, Cui TJ. Reflection and refraction properties of plane waves on the interface of uniaxially anisotropic chiral media. Journal of the Optical Society of America. A, Optics, image science, and vision. 2006 Dec:23(12):3203-7 [PubMed PMID: 17106477]
Moore M, Loughman J, Butler JS, Ohlendorf A, Wahl S, Flitcroft DI. Application of big-data for epidemiological studies of refractive error. PloS one. 2021:16(4):e0250468. doi: 10.1371/journal.pone.0250468. Epub 2021 Apr 23 [PubMed PMID: 33891638]
Level 2 (mid-level) evidenceFlitcroft DI. Emmetropisation and the aetiology of refractive errors. Eye (London, England). 2014 Feb:28(2):169-79. doi: 10.1038/eye.2013.276. Epub 2014 Jan 10 [PubMed PMID: 24406411]
Kaur K, Gurnani B. Prisms. StatPearls. 2023 Jan:(): [PubMed PMID: 35593813]
Cossack M, Salini B. Prism Glasses. StatPearls. 2023 Jan:(): [PubMed PMID: 31082166]
Hatt SR, Leske DA, Liebermann L, Mohney BG, Holmes JM. Variability of angle of deviation measurements in children with intermittent exotropia. Journal of AAPOS : the official publication of the American Association for Pediatric Ophthalmology and Strabismus. 2012 Apr:16(2):120-4. doi: 10.1016/j.jaapos.2011.11.008. Epub [PubMed PMID: 22525165]
Shen J, Clark CA, Soni PS, Thibos LN. Peripheral refraction with and without contact lens correction. Optometry and vision science : official publication of the American Academy of Optometry. 2010 Sep:87(9):642-55. doi: 10.1097/OPX.0b013e3181ea16ea. Epub [PubMed PMID: 20601913]
Schiefer U, Kraus C, Baumbach P, Ungewiß J, Michels R. Refractive errors. Deutsches Arzteblatt international. 2016 Oct 14:113(41):693-702. doi: 10.3238/arztebl.2016.0693. Epub [PubMed PMID: 27839543]
García-Montero M, Felipe-Márquez G, Arriola-Villalobos P, Garzón N. Pseudomyopia: A Review. Vision (Basel, Switzerland). 2022 Mar 4:6(1):. doi: 10.3390/vision6010017. Epub 2022 Mar 4 [PubMed PMID: 35324602]
Shah RY, Agrawal YK. Introduction to fiber optics: Sensors for biomedical applications. Indian journal of pharmaceutical sciences. 2011 Jan:73(1):17-22. doi: 10.4103/0250-474X.89752. Epub [PubMed PMID: 22131617]