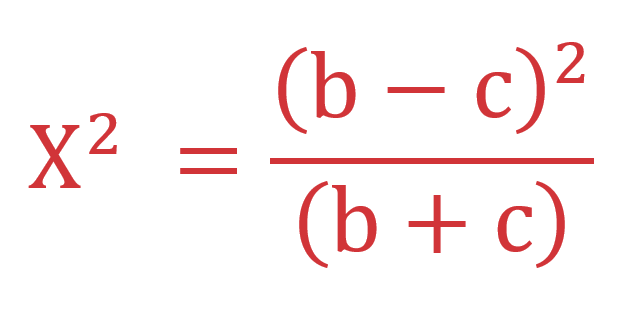Definition/Introduction
All good research is based on a meticulous and well-designed question in the form of a hypothesis. To test this hypothesis, one must conduct an experiment with strict guidelines to obtain robust results. The results are then tested using statistics to examine its significance and conclude if a new treatment/ diagnostic modalities/biomarker is a better alternative to prevalent practice. Thus, statistical tests are an important component of research, especially in the fields of medicine.
Historically, statistical testing has been a grueling and labor-intensive process. Thanks to modernization and the use of computers, statistical analysis can now be accomplished through many commercially available programs, such as the Statistical Program for Social Sciences (SPSS) or Software for Statistics and Data Science (STATA).
Conventionally, statistical tests divide into two major groups, parametric and non-parametric. The prerequisite of using a parametric analysis is that the data tested assumes a normal (Gaussian) distribution. If the data is not in a normal distribution, non-parametric tests are used. There are many non-parametric tests analogous to parametric tests in continuous variables, namely Mann-Whitney U test and independent t-test, Wilcoxon signed-rank test, and paired t-test, Kruskal Wali's test and Analysis of Variance (ANOVA), and Spearman rank correlation coefficient and Pearson product-moment coefficient.[1]
McNemar test
For nominal variables, in the form of a 2 x 2 table, three types of statistical tests can be used. The first one is the Fisher's exact test. The preconditions for its use are binary data and unpaired samples. The second one is the McNemar test, which requires binary data as in Fisher's exact, albeit with paired samples. The third one is the Chi-squared test, requiring a sample size of more than 60 subjects, with more than five counts in each cell. The Chi-squared test can also be useful for a contingency table of more than 2 x 2, i.e., 3 x 3, 4 x 4, and so on.[2]
The McNemar test is a non-parametric test used to analyze paired nominal data. It is a test on a 2 x 2 contingency table and checks the marginal homogeneity of two dichotomous variables. The test requires one nominal variable with two categories (dichotomous) and one independent variable with two dependent groups. Also, the two groups in the dependent variable must be mutually exclusive, i.e., cannot be in more than one group. The minimal sample size required for the McNemar test is at least ten discordant pairs. The formula for calculating the Chi-squared value for McNemar test appears in Image 1, where b is the false positive count, and c is the false negative count.
If the Chi-squared value is significant, the null hypothesis is rejected, meaning there is a substantial difference in the marginal proportions of the tests, i.e., the newer treatment/ diagnostic modalities/biomarker is a better alternative to prevalent practice.
It should be noted that if the sum of discordant pairs (b+c) is small (<25), even if the total sample size is large, the statistical power of the McNemar test is low. Thus, in research studies with small sample size, and the sum of discordant pairs is less than 25, the exact binomial test can be used. Alternatively, Edwards's continuity correction is another option.[3] Nevertheless, the use of an exact test in studies with few subjects will produce unnecessary large p values with poor power.
Therefore, others developed a more precise approach to deal with this situation. The McNemar mid-p test considerably improves the statistical significance without violating the nominal level. Furthermore, if small but frequent violations at the nominal level are acceptable, then the McNemar asymptotic test, is the most powerful test that for this purpose.[4]
Mann Whitney U test
Mann Whitney U test or Wilcoxon Rank-Sum test, on the other hand, is an analog of the parametric Student's t-test. It compares the means between two independent groups with the assumption that the data is not in a normal distribution. Therefore, it is useful for numerical/continuous variables. For example, if researchers want to compare two different groups' age or height (continuous variables), in a study with non-normally distributed data, then the Mann Whitney U test can be used.