Continuing Education Activity
Refractive errors are the second leading cause of global visual impairment. Of the refractive errors, astigmatism is the most common. In understanding astigmatism, the conoid of Sturm is a central concept. The conoid of Sturm is the configuration of rays refracted through an astigmatic (toric) surface. A toric surface has different curvatures of its two meridians. Rays of light passing through such a surface come to focus at two focal lines. The distance separating the two focal lines is called the interval of Sturm. As light is transmitted through the focal elements of the astigmatic eye (the cornea and crystalline lens), it forms a conoid of Sturm. Thus, in-depth comprehension of the conoid of Sturm is important for eye care providers to understand the optics of astigmatism. This activity outlines the role of the interprofessional team in understanding astigmatism to improve care for patients with this condition.
Objectives:
Describe how the astigmatic lens forms the conoid of Sturm.
Outline the principles of refraction of a toric surface.
Explain the optics of astigmatism and understand the types of astigmatism.
Identify the application of the conoid of Sturm in astigmatism.
Introduction
Refractive errors are defined as conditions when the light rays are not focused at a single point on the retina.[1] Refractive errors are now considered the world’s second leading cause of visual impairment, responsible for 43% of global vision loss. Astigmatism is the most common type of refractive error, affecting 40.4% of adults and 14.9% of children. The highest prevalence has been found in America and the lowest in Africa.[2]
Uncorrected refractive errors can produce symptoms such as blurred vision, sore and strained eyes, squinting, feeling of ocular dryness, headache, sensitivity to light, and watering of the eyes.[3] Hence, it is important to understand the optics behind astigmatism and its correction. In this regard, the conoid of Sturm is an important concept. It is named after a famous French mathematician Jacques Charles Francois Sturm (1803-1855).[4]
Function
Definition
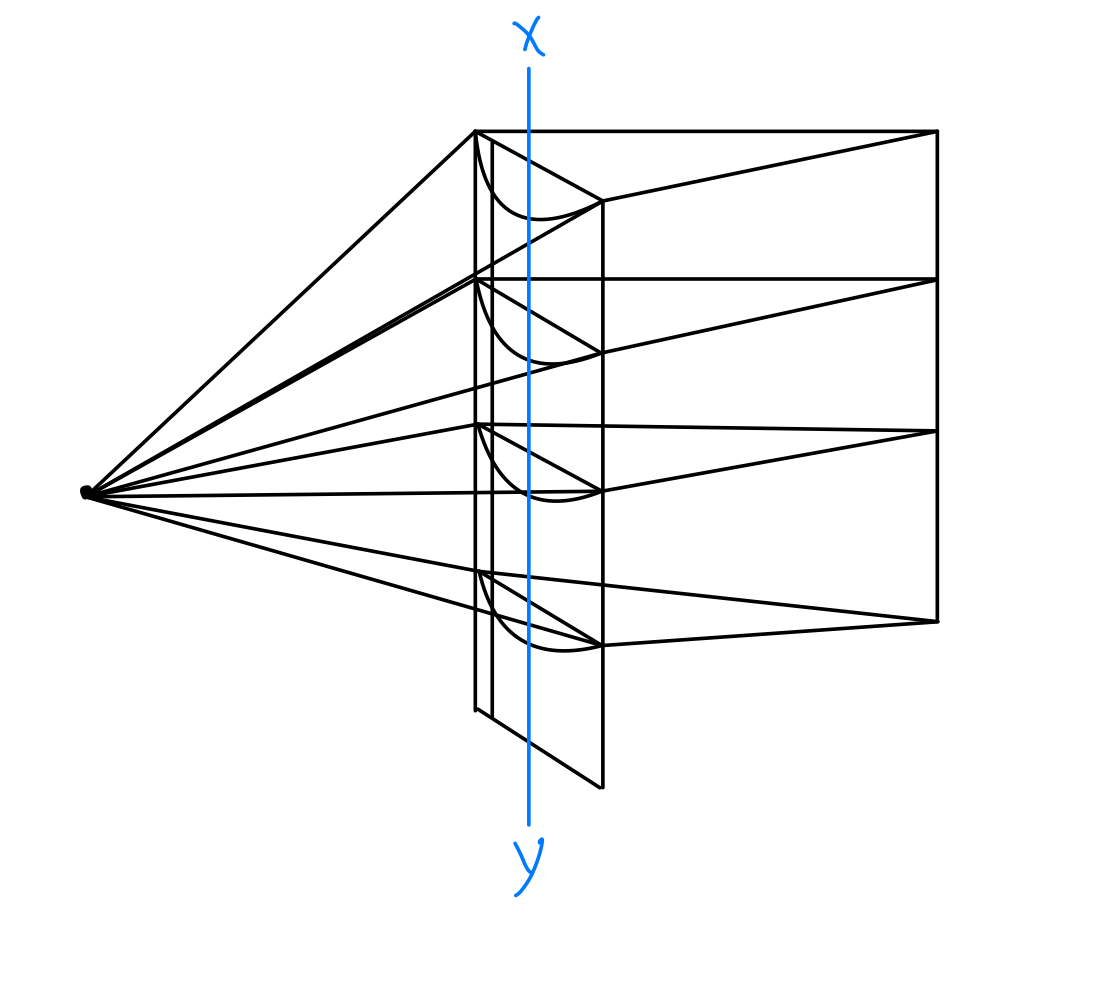
The conoid of Sturm is the configuration of rays refracted through a toric surface. Its main elements are the two focal lines that are created by the two meridians of the toric lens. The distance between the two focal lines is called the interval of Sturm. The circle of least confusion is located halfway between the two focal lines.
What is a toric lens?
Lenses can be of two broad types:
The focusing power of a surface is created by the degree of curvature and the change in the index of refraction. A surface with equal curvature and focusing power throughout the lens is spherical. Light falling through this lens will be focused in a spot of light called a focal point. On the other hand, when the curvature of the surface is unequal, with a maximum curvature in one orientation and a minimum curvature at an orientation that is 90 degrees away, it creates a toric surface.
The points of maximum and minimum curvature are called the two principal meridians of the lens. The two meridians each focusing light in a line 90 degrees away from the orientation of the meridian. The orientation of the focal line is the same as the axis of the power of the meridian that created the focal line. One way of looking at the axis of a refracting surface is to imagine that the meridian can rotate around the axis.
Astigmatic lenses can further be of two types:
- Plano-cylindrical
- Sphero-cylindrical
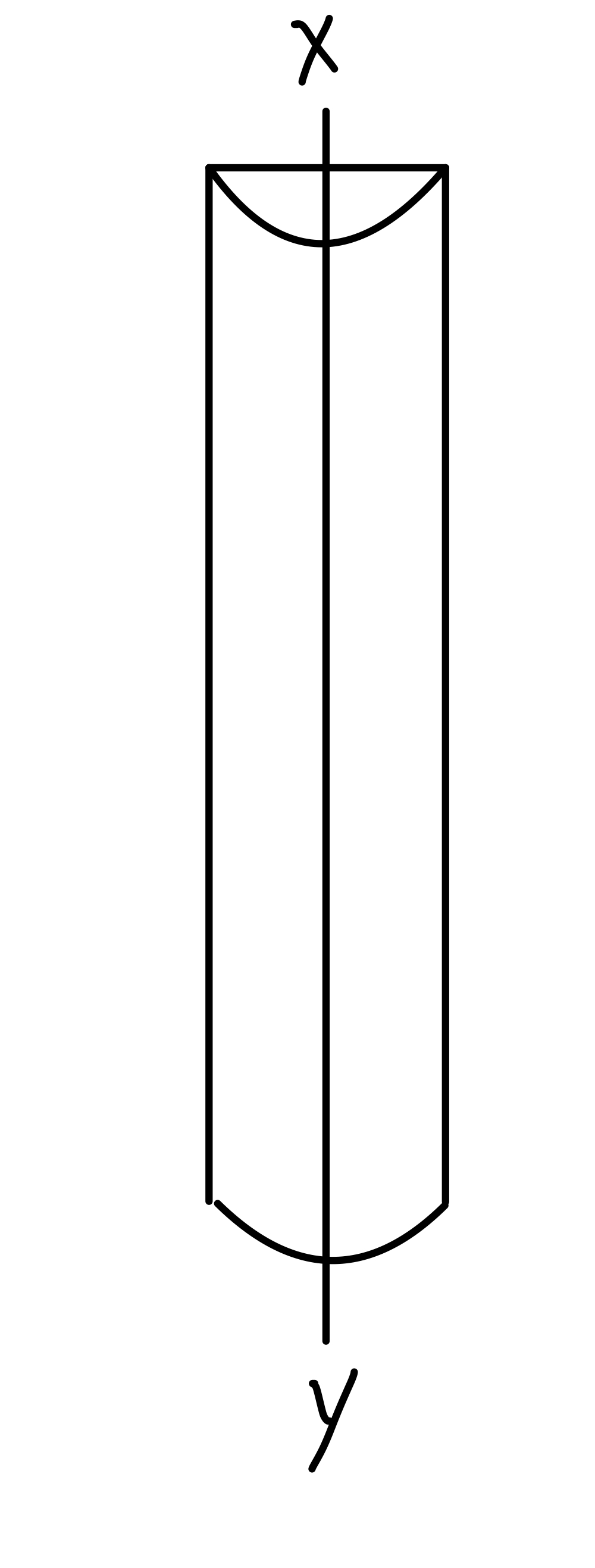
Plano-cylindrical lenses have one meridian that has no focusing power (the Plano meridian) and one meridian that does focus light (the cylindrical meridian). The Plano meridian creates a focal line at infinity, while the cylindrical component creates a focal line at a finite distance. See Figure. A Plano-cylindrical lens. Therefore, in the case of the Plano-cylindrical lens, one of the focal lines is at infinity, and since the circle of least confusion is halfway in between the two focal lines, its location is at infinity (see Figure. Refraction Through a Cylindrical Lens).[5]
In sphero-cylindrical lenses, both meridians have focusing power, and both will create a focal line at a finite distance. The circle of least confusion is halfway between the two focal lines.
When a lens surface is toric, the base curve of the lens is defined as the principal meridian with the minimum curvature. This meridian will form a focal line that is farthest from the lens.
Power of a Toric Lens
Toric lenses can be represented as an optical cross or as a fraction. The optical cross format displays the focusing power (in diopters) of the two meridians written next to two perpendicular lines representing each of the meridians. The fraction format contains the power of one of the meridians as the numerator and the difference in power of the other meridian as the denominator. The numerator is the spherical power, and the denominator is the cylindrical power.
For example, if a toric lens has +4 diopter power in one meridian and +6 diopter power in the perpendicular meridian. This can be considered a +4 diopter spherical lens with a superimposed +2 diopter cylindrical lens. This lens could be represented as +4 DS/+2 DC. The DS designation indicates "spherical diopter," and the DC designation "cylindrical diopter." The power of one meridian is the numerator of the fraction, and the power of the other meridian is the sum of the numerator and the denominator.
The Spherical Equivalent of a Toric Lens
The spherical equivalent of a toric lens is the average focusing power of the lens. It is the average of the two meridional powers (optical cross format) or can be calculated by adding half the denominator (designated DC) to the numerator (designated DS) when using the fraction format.
For example, the spherical equivalent of the lens discussed above would be:
+4 DS + 1/2(+2DC) = +4 + 1 = +5 diopter.
The position of the circle of most minor confusion of the conoid of Sturm can be found by calculating the focal distance of the spherical equivalent power of the astigmatic lens.
Issues of Concern
Refraction Through a Toric Surface
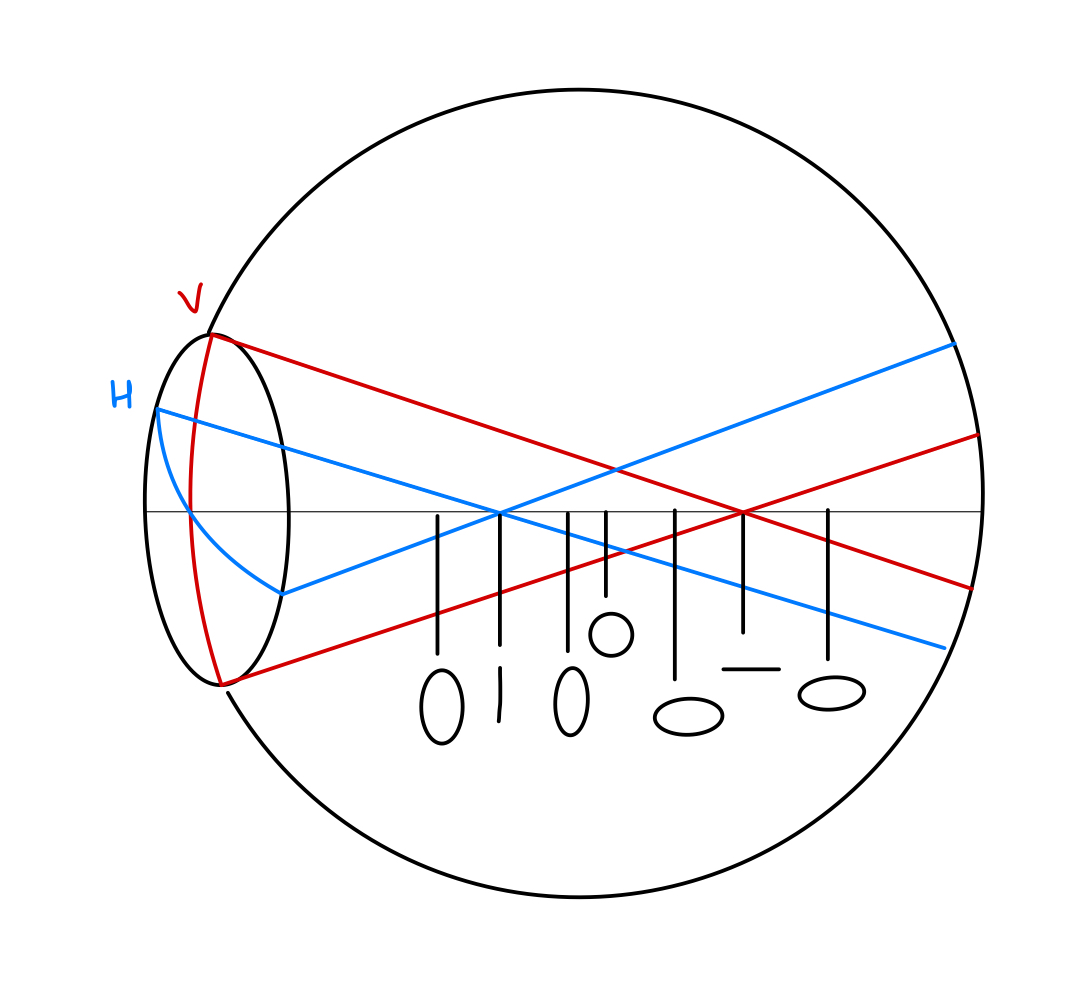
When rays of light pass through a toric surface, they undergo refraction in a configuration referred to as the conoid of Sturm. In the case of a toric surface, where the vertical meridian has a greater focusing power than the horizontal meridian, the vertical rays of light are bent more than the horizontal rays of light. These vertical rays will focus at a point closer to the toric surface than the horizontal rays. Thus, there are two lines of foci that are formed.
The separation between these two focal lines is referred to as the focal interval of Sturm. If a screen is placed at any point other than these two focal lines, the image formed on the screen will be a circle or an oval with varying dimensions.
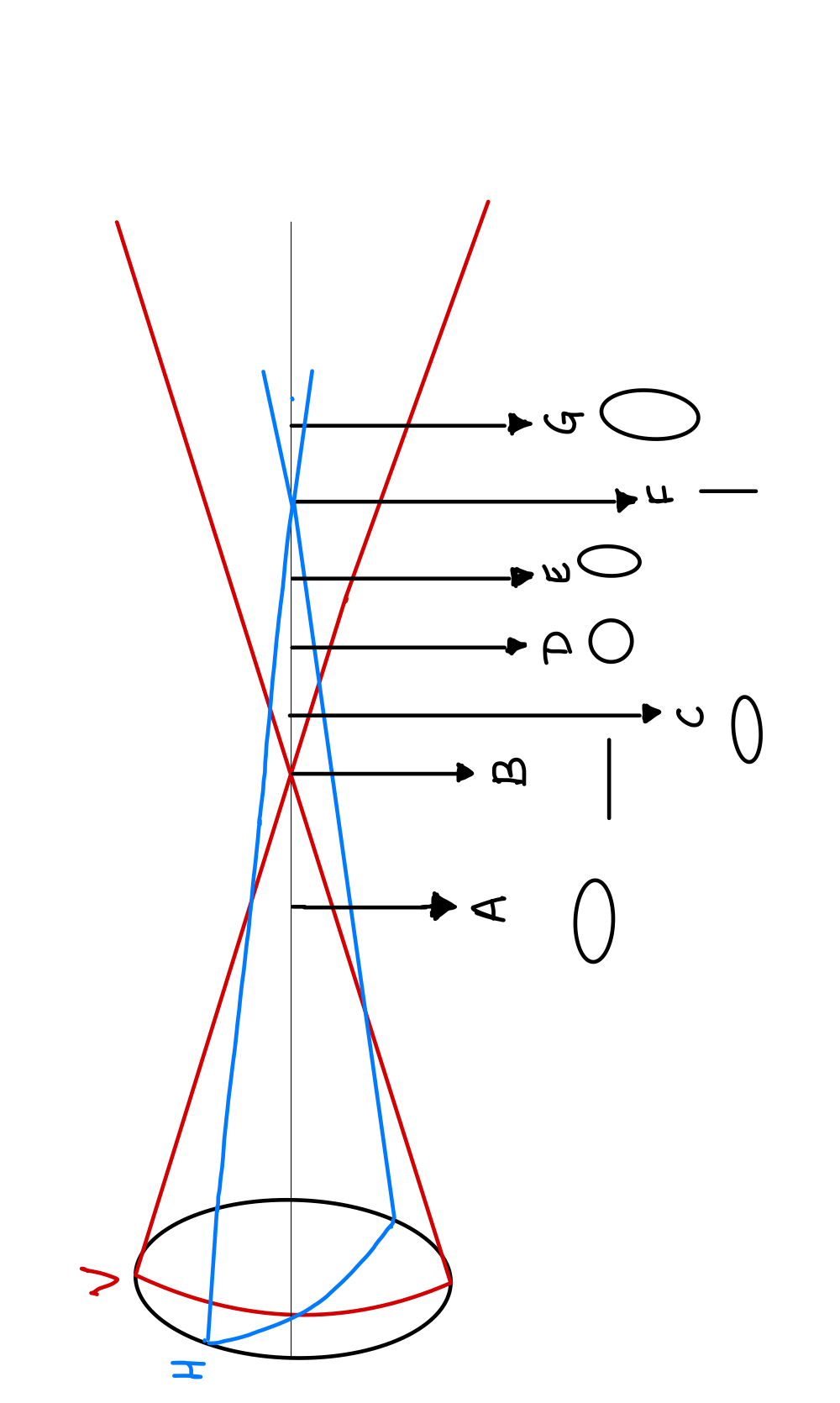
Light images can be recorded at different points within and outside the conoid of Sturm (see Figure. Conoid of Sturm):
- At A, the vertical rays are more converging (as the vertical meridian is more curved) than the horizontal rays. The more converging the rays are, the smaller will be the image produced by them. The image obtained will be an oval with the vertical diameter being smaller than the horizontal diameter, i.e., a horizontal oval ellipse.
- At B, the vertical rays are converged to focus while the horizontal rays are still converging. A horizontal line is formed.
- At C, the vertical rays now start diverging while the horizontal rays are still converging. The amount of divergence of the vertical rays is less than the convergence of the horizontal rays. The image obtained is again a horizontal oval/ oblate ellipse.
- At D, The vertical rays are diverging and horizontal rays are converging. The amount of diverging by vertical rays equals the amount of convergence by the horizontal rays. The image obtained is a perfect circle called the circle of most minor confusion. This is sometimes called the circle of least diffusion.
- At E, the vertical rays are diverging and horizontal rays are converging. The amount of divergence by the vertical rays is more than the amount of convergence by the horizontal rays. The image formed is a vertical oval ellipse.
- At F, The vertical rays are diverging, but the horizontal rays come to focus. The image formed is a vertical line.
- At G, The vertical rays and horizontal rays are diverging. The amount of divergence of the vertical rays is more than the divergence of the horizontal rays. The image obtained is a vertical oval ellipse.
Clinical Significance
The most important application of the conoid of Sturm is the optics and management of astigmatism.
Optics of Astigmatism and The Conoid of Sturm
The same concept can be applied to an eye. In the case of astigmatism, the horizontal and vertical meridians of the eye have different powers. Thus, it becomes a toric surface. The refraction through an astigmatic eye will be configured as the conoid of Sturm. [see image on - Optics of astigmatism and The Conoid of Sturm]. As the light from infinity is not forming a point focus on the retina, the image will be distorted.
Types of Astigmatism and The Conoid of Sturm
Astigmatism can be divided into two types:
Irregular astigmatism is when the power changes non-uniformly from one meridian to another. In this type of astigmatism, the two principal meridians may not be at a perpendicular orientation. This type of astigmatism cannot be corrected with spectacles lenses.[6]
Irregular astigmatism has a variety of causes:
- Irregular corneal surface
- Postoperative causes
- after cataract surgery[13]
- after scleral buckling surgery[14]
- after trabeculectomy[15]
- after LASIK[16]
- after vitrectomy[17]
- Crystalline lens
- Cataract
- Posterior lenticonus[18]
Regular astigmatism is when there is a regular change in power between the two principal meridians.
Regular astigmatism can be further classified in the following ways:
- Based on etiology:
- Corneal astigmatism[19]
- Lenticular astigmatism
- Curvature – Due to congenital abnormalities of the curvature of the lens (for example, lenticonus)
- Positional – tilting of the lens[20]
- Index – due to variable refractive indices within the lens
- Retinal astigmatism - rare and postulated to be formed by unequal meridional lengthening of the sclera within the macula[21]
-
Based on the axis and the position of the axes:
1) With-the-rule astigmatism:
The two principal meridians are placed at right angles. The vertical meridian is more curved than the horizontal meridian (which is in accordance with the regular curvature of the cornea. Normally, the vertical meridian of the cornea is steeper than the horizontal meridian due to pressure from the eyelid hence the name). When light rays from infinity pass through such a system, the rays in the vertical meridian converge more than the rays in the horizontal meridian, forming the conoid of Sturm. [See the image on - Optics of astigmatism and The Conoid of Sturm]
2) Against-the-rule astigmatism:
The two principal meridians are placed at right angles. The horizontal meridian is more curved than the vertical meridian. When light rays from infinity pass through such a system, the rays in the horizontal meridian converge more than those in the vertical meridian, forming the conoid of Sturm (see Figure. Against-the-Rule Astigmatism).
3) Oblique astigmatism:
The two principal meridians are placed at right angles but not in a horizontal/vertical orientation.
4) Bio-oblique astigmatism:
The two principal meridians are not at right angles to each other.
-
Based on the position of the focal lines with respect to the retina:
1) Simple astigmatism:
The rays of light from one meridian focus on the retina, while the rays in the other meridian focus either in front (simple myopic astigmatism) or behind the retina (simple hypermetropic astigmatism). See Figure. Simple Myopic Astigmatism.
2) Compound astigmatism:
The rays of light from both meridians focus either in front of (compound myopic astigmatism) or behind the retina (compound hypermetropic astigmatism)
3) Mixed astigmatism:[22]
The rays of light from one meridian focus in front of the retina, and the rays in the other meridian focus behind the retina.
Optical correction of astigmatism and the conoid of Sturm
The endpoint of refraction in astigmatism is:
1) To ensure that the circle of least confusion falls on the retina:
When the circle of least confusion falls on the retina, the image seen has the least distortion and creates the least perception of blur. To do this, we need to correct astigmatism with a lens with a spherical equivalent equal to the refractive error of the eye and off opposite power.
For example, [See the image on - Using a spherical lens for astigmatism].
2) To collapse the interval of Sturm:
The smaller the circle of least confusion, the clearer the image. But the image is not a point; rather, it is a circle. Therefore, even when the circle of least confusion lies on the retina, the vision is suboptimal. To optimize vision, we need to collapse the conoid of Sturm onto the retina so that the pair of focal lines reduce to a single focal point. This requires using cylindrical lenses to neutralize the error in each meridian. [See the image on - Using a cylindrical lens for astigmatism]
Other Issues
Another application of the conoid of Sturm is the Jackson cross cylinder used in refraction.[23] The Jackson cross cylinder consists of a toric lens mounted on a handle. The meridians of the Jackson cross cylindrical lens have dioptrical powers that are equal but opposite.
For example:
- +1 DS/-2DC
- +1 vertical meridian/-1 horizontal meridian
Therefore, the spherical equivalent of the Jackson cross cylinder will be zero. This implies that, when kept in front of an astigmatic eye, it does not move the circle of least diffusion. It is used to collapse or elongate the conoid of Sturm, which can refine the power and axis of the cylindrical lens that is prescribed to a patient.
Enhancing Healthcare Team Outcomes
Managing astigmatism requires an interprofessional team of healthcare professionals, including optometrists, nurses, ophthalmologists, ophthalmic technicians, and opticians. When a patient walks into the clinic, the nurse and the doctor is responsible for taking a thorough history taking and a complete ophthalmic examination. It includes the following:
- History - Habitual squinting is an attempt to reduce the size of the circle of most minor confusion on the retina. A history of amblyopia, as well as corneal disease or cataracts, can be a cause of astigmatism. A family history of keratoconus or certain corneal dystrophies can increase the suspicion of astigmatism.
- Visual acuity – Distant vision, near vision. A report of letters appearing "three dimensional" or with an associated shadow is indicative of astigmatism and, in essence, a description of the image formed at different locations along the conoid of Sturm.
- Refraction – Subjective and objective. An awareness of the need for objective refractive findings such as autorefraction or retinoscopy is essential, as subjective refraction is often hard in patients with higher amounts of astigmatism.
- Intraocular pressure measurement
- Anterior segment examination. The main causes of astigmatism are caused by the cornea and the crystalline lens.
- Fundus examination. This part of the exam will help rule out posterior segment causes of blurred vision and eliminate the rare occurrence of retinal astigmatisms, such as can, in theory, be caused by a retinal staphyloma or other types of scleral distortion.
Additional testing may be indicated:
- Rigid gas permeable contact lens over-refraction. This test allows the neutralization of corneal astigmatism.
- Corneal topography or keratometry. This test may allow the clinician to detect astigmatism and determine whether it is of the regular or irregular type.
If an organic cause is found, it must be treated accordingly. If not, the patient must then be offered optical correction through spectacles or contact lenses. They must also be offered refractive surgery if they fit the criteria. Regular follow-up visits to check for compliance and progression are equally important in managing astigmatism.