Definition/Introduction

The index of refraction (n) is an essential parameter in optics that determines the speed by which light travels through a medium other than a vacuum. A vacuum, like is present in outer space, is the only medium in which electromagnetic waves experience no dispersion and travel at the speed of light c. Traveling through all other media slows the sine propagation wave of light, and thus the resultant speed is given by the index of refraction: n = speed of light (c) / speed of light in material (v).[1] 

The index of refraction is an important parameter used in optics to determine the angle by which light is reflected and refracted through different materials. It is an intrinsic property that is fundamental in the development of eyeglasses, contact lenses, and optical equipment such as cameras and telescopes.

Issues of Concern

The index of refraction is given by the equation:

• n = c / v
• c = speed of light (~300,000 km/s)
• v = speed of light in a material

Determining the rate at which an electromagnetic wave travels through a non-vacuum substance or the phase velocity, can be difficult considering the multitude of electromagnetic interactions occurring between charged particles. As an incident wave of light enters a dilute gas, its electric field polarizes the electrical field of the gas so that a new sine motion of the electrons is generated. The resultant energy radiates a new field onto the initial electric field, which vibrates out of phase with the original field but at the same frequency. The difference in the vibration phase is the resultant phase velocity by which light travels, thus determining that substance's index of refraction.[2]

While the index of refraction for gas is close to one, the phase velocity of light through a gas is still less than c. As the index of refraction increases, the speed of light is inversely affected. The absolute index of refraction n is given when light travels from a vacuum into another medium, whereas the relative index of refraction is the resultant n when light travels from one non-vacuum medium into another.

Wavelength and Energy Dependency

The refractive index of a material affects the wavelength, energy, direction of propagation, and state of polarization of a ray of light and vice versa.[2][3] The speed of light is given by the equation v = lf, where v is the velocity of light, l is the wavelength, and f is the frequency. Thus, the index of refraction impacts wavelength by the following equation: l = lo /n, where lo is the wavelength of light in a vacuum and l is the resultant wavelength. The index of refraction does not impact the frequency of light as it travels between media. However, the refractive index does vary with the wavelength of light, and different wavelengths are bent at different angles.[4]

This wavelength dependency illustrates that as the wavelength of light increases, the index of refraction decreases; this is known as the dispersion property of a material.[4][5] Clinically, different colors of light are refracted through materials differently, such that shorter wavelengths (such as blue) will experience a greater refractive index per material as compared to a color of a longer wavelength (red, for example).[4]

Temperature, or energy, may also impact the refractive index as higher temperatures increase the kinetic energy of materials, thus decreasing the density. The resultant refractive index decreases as light can travel faster in a less dense medium than in that same medium at a lower temperature.[6] 

Changes in refractive index with temperature are largely due to temperature dependence of the electronic polarizability that occurs at constant volume.[6] It is also theorized that the scattering of light in solids causes changes in refractive index due to changes in density and temperature.

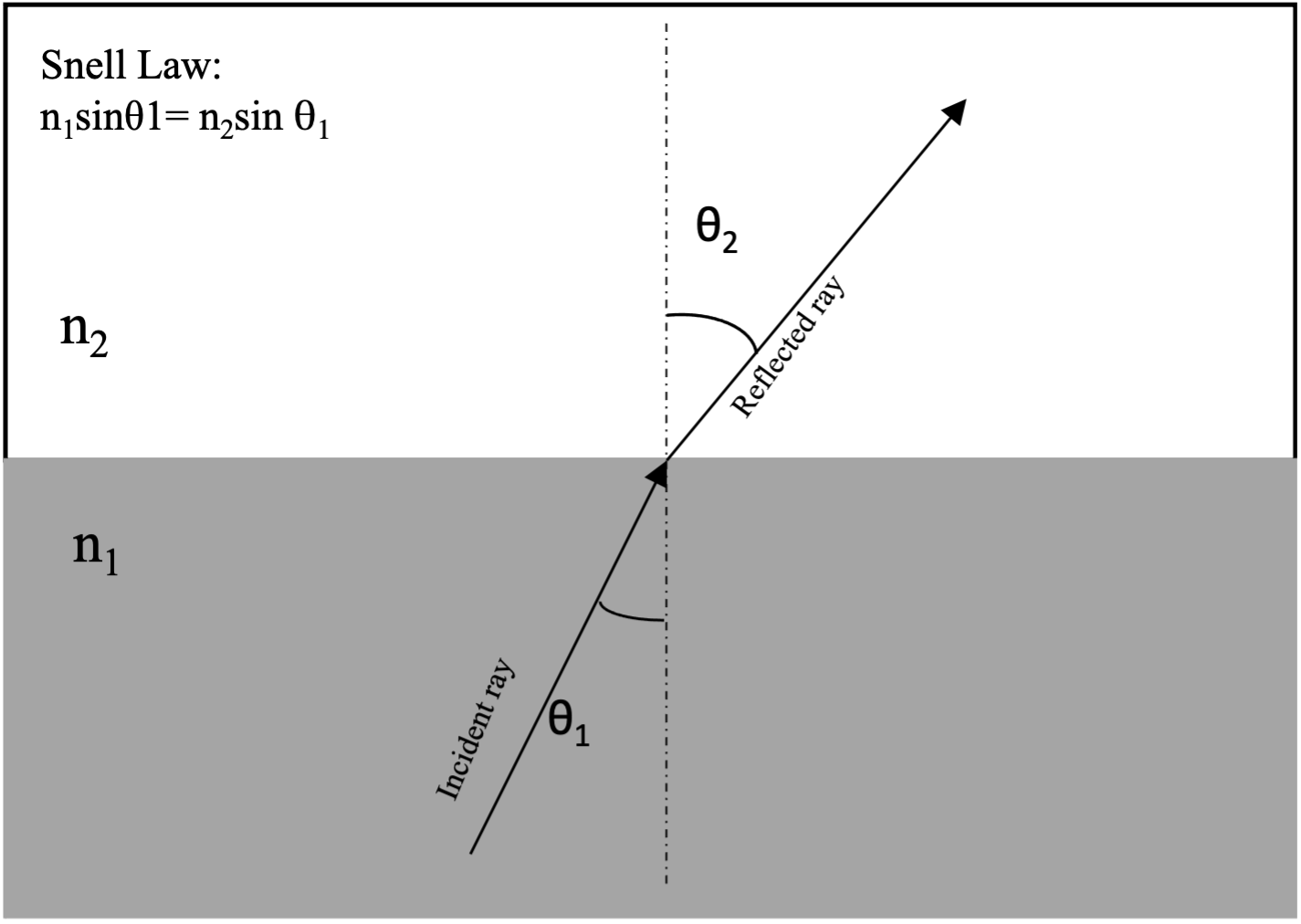
Snell Law

The direction of propagation of a beam of light and the index of refraction interplay as shown in Snell's law, or the law of index of refraction.

 Snell law is given by the equation:

• n1sin(theta1)= n2sin(theta2)
• n1= index of refraction of medium 1
• n2= index of refraction of medium 2
• theta1= angle of incidence
• theta2= angle of refraction

The law of the index of refraction states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant when traveling from one media to another. Light travels in the path requiring the shortest amount of time, as determined by Snell Law, which is faster via refraction than by traveling in a straight line.[7]

When assessing a light beam's refraction, the angle of incidence and refraction are measured relative to the "normal." The "normal" is a line perpendicular (at 90 degrees) to the surface at which the refraction occurs. When traveling into a denser material, light is bent towards the normal. Similarly, light is bent away from the normal when traveling into a material with a lower refractive index. Differences in refractive index thus impact the angle of refraction of the resultant light beam and change the direction of propagation of light.

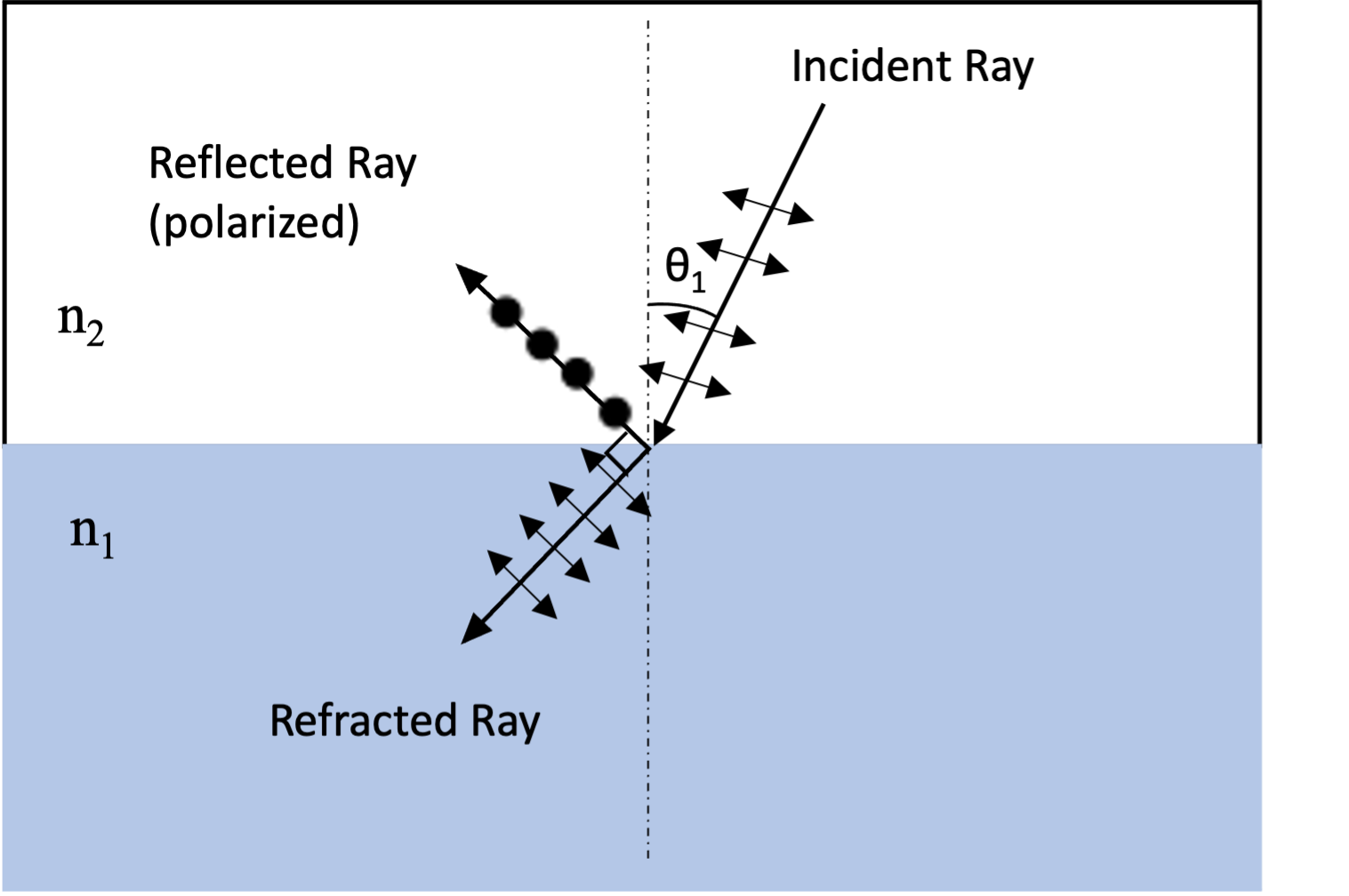
Brewster Law

Brewster's law states that as light travels through a medium, it is polarized so that the tangent of the angle of polarization is the index of refraction of the medium.[8] The refracted and the reflected rays of polarized light are perpendicular to one another, so a light beam will be linearly polarized if reflected perfectly perpendicular to the refracted beam.[9]

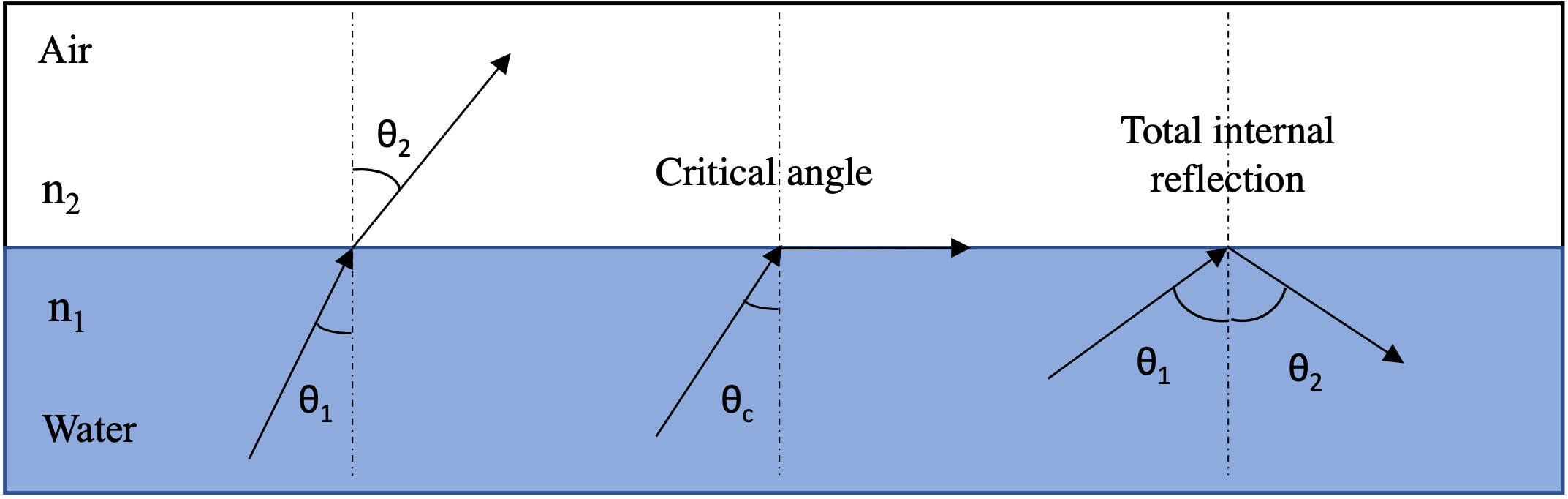
Critical Angle and Total Internal Reflection

There may be a circumstance in which a beam of light is completely reflected back into the original medium. This occurs when Snell law cannot be fulfilled, and an angle θ2 cannot exist because the incident angle is larger than the critical angle or the angle of maximum refraction. At this specific incident angle, the reflectivity of light is significantly reduced so that the light energy is not refracted into the second medium and instead undergoes total internal reflection into the original medium.[10]

Light cannot be transmitted as the angle of incidence is larger than the critical angle, such as when going to a much less optically dense material with a lower refractive index. The critical angle is given by (theta)c= arcsin (n2/n1). As the incident angle increases towards a medium, the refracted angle gets closer to the surface of the angle. Given the equation for the critical angle, the limit for the refracted angle is 90 degrees. Therefore, the critical angle is reached when the angle of refraction reaches 90 degrees. For incident angles larger than the critical angle, the refracted angle would be greater than 90 degrees, so the resultant light undergoes total internal reflection.[10]

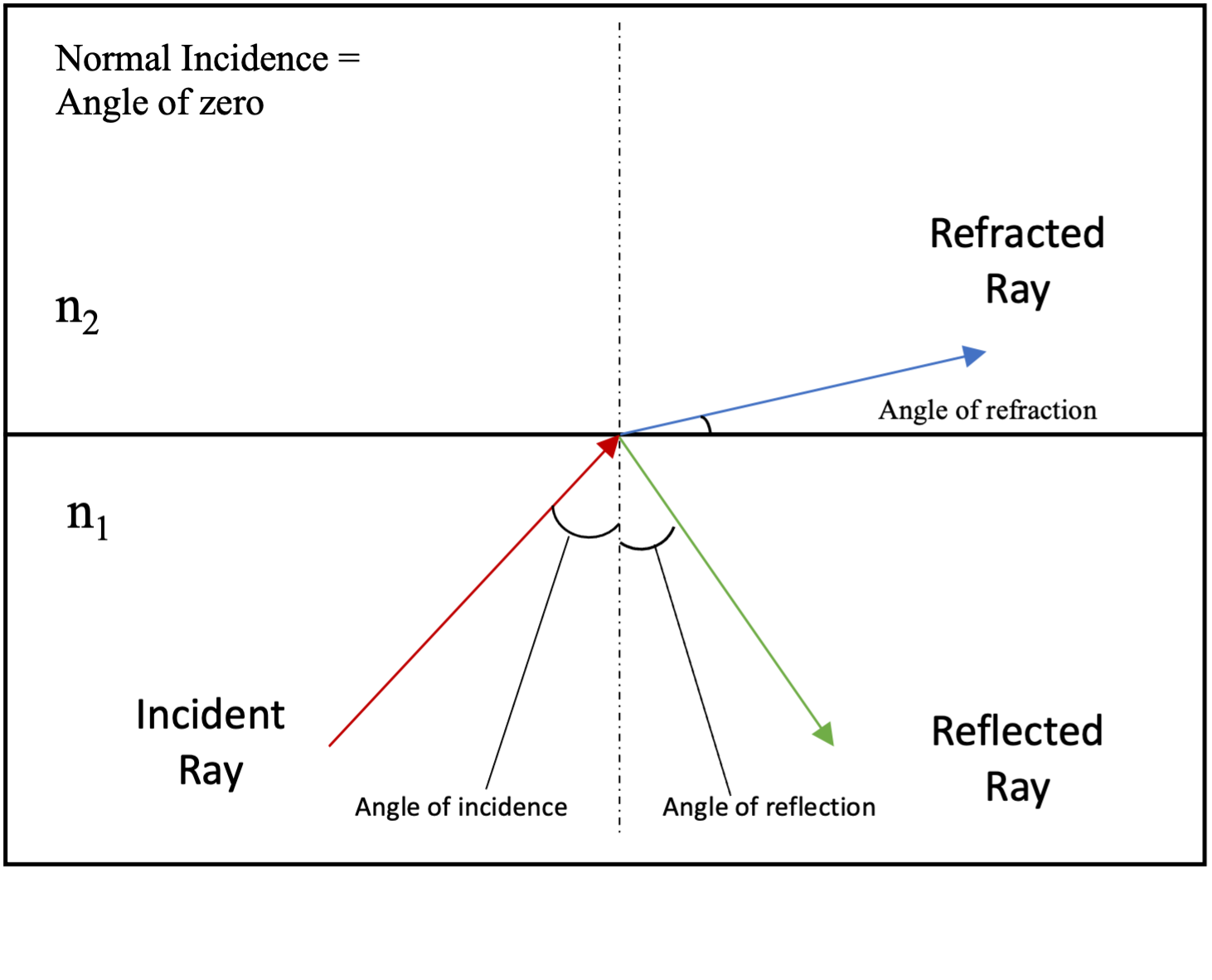
Reflection and Normal Incidence (Fresnel Equations)

The Fresnel Equations describe the interplay between reflection and index of refraction by discussing the ratio of transmitted light versus reflected light. When a mismatch occurs between the refractive index of two media, partial reflection of light occurs at the boundary.[11] 

The intensity of the specular reflection of a material depends on both the refractive index of the material and the viewing angle or angle of the surface.[12] Wavelength dependency also impacts the reflectivity of a substance as light with a shorter wavelength bends more due to the larger refractive index it experiences, as discussed previously in wavelength dependency.[13] Materials that appear "glossy" or highly reflective, like a mirror, tend to have a refractive index in a narrow range between water (1.33) and glass (1.7) in typical environments.[12] 

Polarization of light also plays an important role in reflection; however, at normal incidence (when the light beam is parallel to the normal and perpendicular to the surface), polarization does not play a role in reflectance. At normal incidence, reflectance is greatest when traveling from a material with a much higher refractive index into a much lower one.

Clinical Significance

Understanding applications of the index of refraction in optics, optometry, and ophthalmology is vital for achieving the ideal refraction and clarity of vision. The human eye is a complex system of refracting surfaces, including the cornea and crystalline lens. The cornea, aqueous humor, crystalline lens cortex and nucleus, and vitreous humor all have their respective refractive indices, and each can cause or neutralize spherical aberrations in the human eye as these different structures age.[14] 

The cornea has a refractive index of 1.37, and the lens varies from a maximum index of refraction at the core of 1.42 to a minimum of 1.37 at the lens surface.[15][16] This power of the gradient is independent of the surface powers of the lens; thus, the total refracting power of the crystalline lens is greater than the sum of the surface powers.[17] The refractive index of the crystalline lens increases with age, resulting in changes in refractive error.[18] 

Multiple optical models of the human eye have been developed using these principles to explain optical phenomena and predict refractions in human eyes. The current lenticular theory postulates that presbyopia occurs as a result of changing optic parameters over time, including the growth of the crystalline lens, changes in mean refractive index, and changes in surface refractive index.[19]

Eyeglasses

The use of spectacles to correct myopia and presbyopia dates back to the 13th century, but it was not until the 17th century that Willebrord Snell described the relationship between the angles of incidence and refraction, and the optics behind spectacles were understood.[17] This relationship, described by Snell's Law, is utilized to select the proper lens for the eyes. As discussed earlier, the refractive index of a material is dependent on the physical properties and electrical permittivity of the substance, so refractive indices vary among different types of lenses.[3]

Conventional lenses found in today's eyeglasses are made of glass or plastic with fixed focal lengths dependent on the refractive index, curvature, and thickness of the lenses.[20] Regular plastic and glass lenses tend to have a refractive index of around 1.5.[21]

High-index lenses have a much higher index of refraction, often between 1.61 and 1.74, to provide similar refractive power as conventional glasses but with a much thinner lens. This is beneficial for patients with high prescription powers. In general, as the refractive index increases, the thickness of the lens decreases. Lastly, different coatings can be added to glasses to achieve different features and cosmetic looks by layering materials with different refractive indexes. High-index lenses, which have a much higher refractive index than traditional lenses, will also reflect more light, and thus, anti-reflective coatings can be applied to reduce this feature. The anti-reflective coating should ideally have a refractive index in between that of air and the material of the high-index lens and be equal to the square root of the lens' refractive index for minimal reflection.[22] 

Contact Lenses

Contact lenses are small, artificial devices placed on the eyes that use the inherent properties of lenses to provide correct, refracted vision.[15] The refractive index of contact lenses depends on the density of the lens, and the ideal refractive index is to be close to that of the tear film, 1.33.[15] The tear film of the eye fills in irregularities on the surface of the cornea so that there is a uniform surface for refraction, and a contact lens is designed to function similarly.[15]

The refractive index of a contact lens dictates the material it is made from. Contact lenses with a refractive index of less than 1.458 are generally made from a material called fluoro silicone acrylates.[23] For a refractive index above 1.469, lenses are typically made with silicone acrylates.[23] Lenses with a refractive index between these two values can be made from either material.[23]

Intraocular lenses

PMMA, silicone, and acrylic intraocular lenses (IOLs) consist of materials that vary in the index of refraction between 1.40 and 1.56.[24] The index of refraction determines the thickness of the IOL and can impact surgical outcomes such as the risk of post-surgical glare from internal and lens-edge reflections.[25] 

Intraocular lens power calculations depend on certain assumptions that are made with regard to the index of refraction of the cornea. In the case of an eye that has undergone refractive surgery, this assumption is incorrect, and several adjusted IOL power calculation methods have been developed for these types of eyes.[26] 

While most monofocal and multifocal intraocular lenses have constant refractive index throughout the lens, the Fyodorov Gradiol or gradient refractive index optics multifocal IOL has been designed with variable refractive index. This lens may provide less glare compared to the diffractive type of multifocal IOL.[19]

Telescope

The refractive index of air plays an important role in the design of ground-based optical telescopes. To avoid the impact of harmful weather patterns, most telescopes are housed within a glass or plastic dome, creating a temperature, pressure, and speed of air that is of atypical distribution and a resulting refractive index of air that has a nonuniform distribution.[27]

This scenario results in a phenomenon called "dome seeing," in which the quality of the image through the telescope is degraded.[27] Because the image's quality depends on a homogenous refractive index of the air through which light travels, changes in temperature and speed of air around the dome impact the refractive index most.

Microscopy and Optical Coherence Tomography

The refractive index is used in several medical imaging systems and devices to create optical contrast among tissue samples, making other dyes and labels unnecessary.[3] Like gas, liquids, and glass, all tissues have an intrinsic index of refraction, which can be analyzed in computed tomography (CT) or optical coherence tomography (OCT) to create contrast and derive meaning from the images produced.[3]

These techniques can also be used in confocal reflectance microscopy, light scattering spectroscopy, and quantitative phase microscopy to derive structural or morphological features of samples.[5] As the refractive index of light is wavelength dependent, the dispersion property of material may impact microscopy, though most biomolecules do not have significant dispersion in the visual wavelengths of light.[5] However, this dispersion property can be used to determine the concentration of hemoglobin in red blood cells in vivo, for instance.[5]

Nursing, Allied Health, and Interprofessional Team Interventions

The interprofessional healthcare team should understand the refractive index to enhance patient outcomes and satisfaction regarding proper eyeglasses and contact lens fittings. This coordination involves various professionals, including ophthalmologists, optometrists, opticians, optical technologists, and nurses. A key aspect to consider is the refraction of light to achieve proper focus on the macula of the eye based on measurements and assessments conducted by ophthalmologists or optometrists.

Based on these measurements, opticians and optical technologists play a crucial role in assisting patients in selecting appropriate glasses and contact lenses. For patients with high prescription needs, healthcare team members should inform them about different lens materials, such as high-index lenses that utilize a higher refractive index to achieve thinner spectacle lenses overall.

Different eyeglass materials also have different reflectivity. Opticians and technologists can guide patients on their preferred cosmetic look by applying coatings or changing materials that alter the refractive index and reflectivity. High-index lenses reflect more light than lower-index lenses due to the higher refractive index in these lenses as a consequence of the Fresnel equations.[22] Thus, it can be beneficial to layer an antireflective coating in these glasses with a refractive index between that of the glasses and air, as this will reduce the light reflection from the surface of the glasses.[22]